Table of Contents
Introduction
A graph \(G\) is composed of nodes \(V\) and edges \(E \subseteq V \times V\). Without any loss of generality, let's assume that the nodes are integers, it's always possible to define a bijective mapping between nodes and integers.
\[ E = \left\{ (0, 1), (0, 7), (0, 8), (1, 3), (1, 8), (2, 4), (2, 9), (4, 6), (4, 9), (5, 3), (6, 5), (6, 8),
(7, 2), (7, 5), (9, 3) \right\}\]
Edge encoding
In order to encode a graph using elias-fano we need to define a bijective-mapping between the edges and integers. There are many possible encodings.
\[\phi(src, dst) = \left(src \times |V|\right) + dst\]
\[\begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ \end{bmatrix}\]
\[\begin{bmatrix} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9\\ 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19\\ 20 & 21 & 22 & 23 & 24 & 25 & 26 & 27 & 28 & 29\\ 30 & 31 & 32 & 33 & 34 & 35 & 36 & 37 & 38 & 39\\ 40 & 41 & 42 & 43 & 44 & 45 & 46 & 47 & 48 & 49\\ 50 & 51 & 52 & 53 & 54 & 55 & 56 & 57 & 58 & 59\\ 60 & 61 & 62 & 63 & 64 & 65 & 66 & 67 & 68 & 69\\ 70 & 71 & 72 & 73 & 74 & 75 & 76 & 77 & 78 & 79\\ 80 & 81 & 82 & 83 & 84 & 85 & 86 & 87 & 88 & 89\\ 90 & 91 & 92 & 93 & 94 & 95 & 96 & 97 & 98 & 99\\ \end{bmatrix}\]
\[\phi(E) = \begin{bmatrix}1 & 7 & 8 & 13 & 18 & 24 & 29 & 46 & 49 & 53 & 65 & 68 & 72 & 75 & 93 \end{bmatrix}\]
Properties
To provide real-world examples, in this section I'm going to reference some real world graphs:
| Graph | # nodes | # edges | Density \(\delta\) |
|---|---|---|---|
| Twitter2010 | 41M | 1.5G | \(8.46 \times 10^{-7}\) |
| Wikidata | 1.2G | 12.4G | \(8.61 \times 10^{-9}\) |
| Facebook2011 | 0.72G | 127G | \(2.64 \times 10^{-7}\) |
| GoogleKG | 5G | 500G | \(2.00 \times 10^{-8}\) |
Space usage
From the previous post we know that: \[\mathcal{EF}(u, n) \le 2n + n \left \lceil \log_2 \frac{u}{n} \right \rceil\]
With this encoding we get:
\[\mathcal{EF}(|V|, |E|) \le 2|E| +|E| \left \lceil \log_2 \frac{|V|^2}{|E|} \right \rceil\]
| Graph | EF | Bits per edge |
|---|---|---|
| Twitter2010 | 4.2GB | 23 |
| Wikidata | 44.95 GB | 29 |
| Facebook2011 | 411.98 GB | 24 |
| GoogleKG | 1.75 TB | 28 |
CSR representation
A CSR representation needs:
\[CSR(|V|, |E|) = |V| \left\lceil\log_2|E|\right\rceil + |E| \left\lceil\log_2|V|\right\rceil\]
On common implementations, 64-bit integers are used for the cumulative node degrees, and either 32-bit or 64-bit integers depending on the size of the graph, which results in:
| Graph | Ideal CSR | Bits per edge | Real CSR | Bits per edge | Overhead ratio |
|---|---|---|---|---|---|
| Twitter2010 | 4.9GB | 26.88 | 6.2GB | 33.8 | 26% |
| Wikidata | 53.1 GB | 34.29 | 59.2 GB | 38.19 | 11% |
| Facebook2011 | 518.30 GB | 30.19 | 555.1GB | 32.34 | 7% |
| GoogleKG | 2.1 TB | 33.39 | 4 TB | 64.64 | 93.59% |
Note that the GoogleKG has an huge overhead because needing around 34 bits to encode an edge, we are going to use 64-bits, thus we would waste 30 bits.
Space savings compared to a CSR
Space saving comapred to a CSR:
\[\begin{align*} CSR(|V|, |E|) - \mathcal{EF}(|V|, |E|) &= |V| \left\lceil\log_2|E|\right\rceil + |E| \left\lceil\log_2|V|\right\rceil - 2|E| - |E| \left \lceil \log_2 \frac{|V|^2}{|E|} \right \rceil\\ &=|V| \left\lceil\log_2|E|\right\rceil + |E| \left( \left\lceil\log_2|V|\right\rceil - 2 - \left \lceil \log_2 \frac{|V|^2}{|E|} \right \rceil\right)\\ &\approx|V| \log_2|E| + |E| \left( \log_2|V| - 2 - \log_2 \frac{|V|^2}{|E|}\right)\\ &\approx|V| \log_2|E| + |E| \left( \log_2|V| - 2 - 2\log_2 |V| + \log_2|E|\right)\\ &\approx|V| \log_2|E| + |E| \left( \log_2|E| - \log_2|V| - 2\right)\\ &\approx|V| \log_2|E| + |E| \log_2 \frac{|E|}{4|V|}\\ \end{align*}\]
Therefore, as long as \(|E| \ge 4 |V|\) we are guaranteed to save memory!
In practical implementations of CSR, instead of \(\left\lceil\log_2|V|\right\rceil\) most libraries use either \(k = 32\) or \(k = 64\) bits integers. Therefore, if we define the graph "density" as \(\delta = \frac{|E|}{|V|^2}\), we get that: \[ \begin{align*} k &\ge 2 - \left \lceil \log_2 \delta \right \rceil\\ k - 2 &\ge - \left \lceil \log_2 \delta \right \rceil\\ 2 - k &\le \left \lceil \log_2 \delta \right \rceil\\ \frac{1}{2^{k - 2}} &\le \delta\\ \end{align*} \]
Therefore for the 32-bit and 64-bit cases we are guaranteed to save memory as long as: \[\delta \ge \frac{1}{2^{30}} \approx 9.32 \times 10^{-10} \qquad \delta \ge \frac{1}{2^{62}} \approx 2.17 \times 10^{-19}\]
Summary
| Graph | EF | Ideal CSR | Compression Ratio | Real CSR | Compression Ratio |
|---|---|---|---|---|---|
| Twitter2010 | 4.2 GB | 4.9 GB | 16.8% | 6.2GB | 47% |
| Wikidata | 44.95GB | 53.15GB | 18.2% | 59.2GB | 31% |
| Facebook2011 | 411.98GB | 518.3GB | 25.8% | 555GB | 35% |
| GoogleKG | 1.75TB | 2.1TB | 19.2% | 4 TB | 130% |
Elias Fano allows us to save around 20% of memory compared to an ideal CSR and around 35% on a real CSR.
Out-Degree of a node
Neighbours
A faster edge encoding
A really simple and fast is to just concatenate the binary representations:
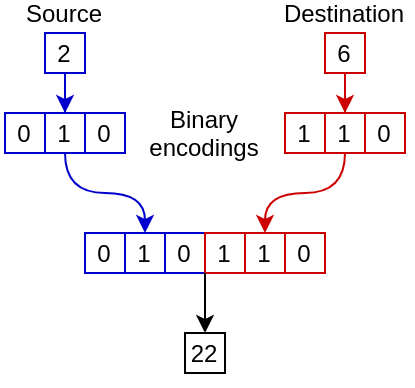
which mathematically is equivalent to:
\[\phi(src, dst) = \left(src \times 2^{\lceil \log_2 |V|\rceil}\right)+ dst\]
fn encode_edge(src: u64, dst: u64, shift: u64) -> u64 {
(src << shift) | dst
}