Table of Contents
Introduction
In this post we will tackle the problem of indexing a set \(X\) of positive integers that takes values in the range \(0 \le x \le u \quad \forall x \in X\) for a given upper-bound \(u\).
Our goal is to store this set in as little memory as possible and to have the following two operations in \(\mathcal{O}(1)\) (constant time):
- \(\text{rank}(X, v)\) returns the number of values in \(X\) that are strictly smaller than \(v\)
- \(\text{select}(X, i)\) returns the \(i\)-th smallest value in \(X\)
These two operations were introduced by Jacobson in its influential paper and were originally meant to simulate a tree, but they are generally usefull and fundamental operations for all succint data-structures.
To be more precise, we are searching for a succint data-structure, which is a representation that allows for fast rank and select and uses \(Z + o(Z)\) bits, where \(Z\) is the information-theoretical minimum space required.
Theoretical Lowerbound
Before thinking about the data-structure we should have to compute the theoretical minimum number of bits \(Z\) required for our task using Shannon's entropy. Shannon's tells us that the entropy \(\mathbb{H}(X_S)\), measured in bits, of a random variable \(X_S\) that has support over a set \(S\) of element \(s \in S\) with probability \(P(s)\) is: \[\mathbb{H}(X_S) = \left \lceil -\sum_{s \in S} P(s) \log_2 P(s) \right \rceil \quad \text{bits}\]
We cannot make any assumption over the probability of each possible set we want to store and index. Thus, we have to consider the most entropic discrete distribution, i.e. an uniform distribution \(P(s) = \frac{1}{|S|} \quad \forall s \in S\). In this particular condition, the entropy of our random variable greatly simplify:
\[\begin{aligned} \mathbb{H}(X_S) &= \left \lceil -\sum_{s \in S} \frac{1}{|S|} \log_2 \frac{1}{|S|} \right \rceil \\ &=\left \lceil - \log_2 \frac{1}{|S|} \right \rceil\\
&= \left \lceil \log_2 |S| \right \rceil \text{bits} \end{aligned}\]
So the next step is to figure out what's the cardinality of our set \(|S|\), which is the set of all the possible sets of integers with \(|X|\) values between \(0\) and \(u\). If we don't allows for duplicates, this can be thought as how many ways we can extract \(n = |X|\) values for a set of \(u\) elements. This is a classical combinatorial problem so we know that \(|S| = \binom{u}{n}\). So finally we obtain that:
\[Z = \mathbb{H}(X_S) = \left \lceil \log_2 \binom{u}{n} \right \rceil \quad \text{bits}\]
To be able to better understand how many bits these are, we can asymptotically simplify it using the binomal coefficient definition and Stirling's approximation to all the factorials:
\[\log_2 \binom{u}{n} = \log_2 \frac{u!}{n!(u-n)!}\qquad\qquad n! \sim_{n \to \infty} \sqrt{2\pi n } \left (\frac{n}{e} \right)^n \]
\[\log_2 \binom{u}{n} \sim_{u, n \to \infty} \log_2 \frac{\sqrt{2 \pi u} \left ( \frac{u}{e} \right)^u}{\sqrt{2 \pi n} \left ( \frac{n}{e} \right)^n \sqrt{2 \pi (u - n)} \left ( \frac{(u - n)}{e} \right)^{(u - n)}}\]
Now hold your breath and let's do some arithmetic simplifications:
\[\begin{aligned} \log_2 \binom{u}{n} &\sim_{u, n \to \infty} \log_2 \frac{\sqrt{u} u^u e^{-u}}{\sqrt{n} n^n e^{-n} \sqrt{2 \pi} \sqrt{u - n} (u - n)^{(u - n)} e^{n - u}} \\ &\sim_{u, n \to \infty} \log_2 \frac{\sqrt{u} u^u}{\sqrt{2 \pi} \sqrt{n} n^n \sqrt{u - n} (u - n)^{(u - n)}} \\ &\sim_{u, n \to \infty} \log_2 \frac{1}{\sqrt{2 \pi}} \sqrt{\frac{u}{n (u - n)}} \frac{u^u}{n^n (u - n)^{(u - n)}} \\ &\sim_{u, n \to \infty} \log_2 \frac{1}{\sqrt{2 \pi}} + \log_2 \sqrt{\frac{u}{n (u - n)}} + \log_2 \frac{u^u}{n^n (u - n)^{(u - n)}} \\ &\sim_{u, n \to \infty} -\frac{1}{2} \log_2 2 \pi + \frac{1}{2}\log_2 \frac{u}{n (u - n)} + \log_2 \frac{u^u}{n^n (u - n)^{(u - n)}} \\ &\sim_{u, n \to \infty} -\frac{1}{2} \log_2 2 \pi + \frac{1}{2}\log_2 u - \frac{1}{2}\log_2 (u - n) + u \log_2 u - n \log_2 n - (u - n) \log_2 (u - n) \\ &\sim_{u, n \to \infty} u \log_2 u - n \log_2 n - (u - n) \log_2 (u - n) -\frac{1}{2} \log_2 2 \pi + \frac{1}{2}\log_2 u - \frac{1}{2}\log_2 (u - n) \\ &\qquad+ (u -n) \log_2 u - (u - n) \log_2 u \\ &\sim_{u, n \to \infty} n \log_2 \frac{u}{n} + (u - n) \log_2 \frac{u}{u - n} + \frac{1}{2} \log_2 \frac{u}{(u - n)} - \log_2 \sqrt{2 \pi} \\ \end{aligned}\]
Now we can exploit the simmetry and only consider the case where \(n \le \frac{u}{2}\) without any loss of generality (we can always choose to store the smallest set between \(X\) and \([0, u] \setminus X \)):
\[\begin{aligned} &\sim_{u, n \to \infty} n \log_2 \frac{u}{n} + (u - n) \log_2 \frac{u}{u - n} + \mathcal{O}(\log u) \\ &\sim_{u, n \to \infty} n \log_2 \frac{u}{n} + \mathcal{O}(n) \end{aligned}\]
Therefore, we finally obtain that:
\[Z \sim_{u, n \to \infty} n \log_2 \frac{u}{n} + \mathcal{O}(n)\] It can be trivially proved that in this context the ceil does not change the complexity
Noticing that \(u / n\) is the average gap between two successive values in the set, we can interpret this result as:
The best way we have to save a set of unsorted integers is to encode the gaps between the values in the set.
Elias-Fano
There's a data-strcutrue introduced by Sebastiano Vigna called EliasFano Index which, based on the work of Perer Elias and Rober Fano on instantaneous code, allows us to solve our task using memory which is close to the lower-bound we found and it's called Elias-Fano.
This encoding sort the values and split, using an optimal threshold \(l\), their binary encoding (\(\lceil \log_2 u \rceil\) bits) into lower bits (\(l\) bits) and higher (\(\lceil \log_2 u \rceil - l\) bits) bits. The low bits are stored contiguosly, while the gap between the high-bits are stored using the inverted unary encoding.
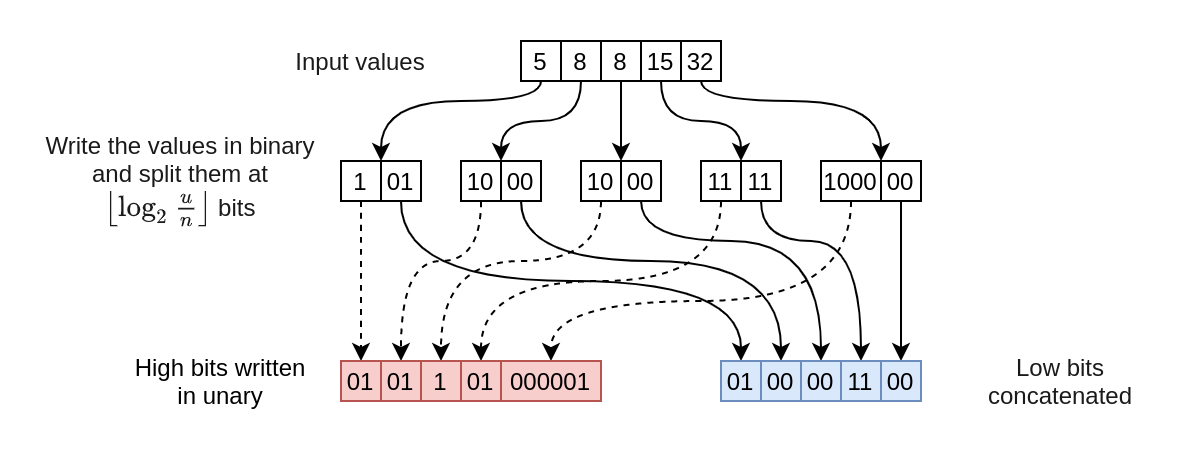
Lower Bits \(L\)
The lower \(l\) bits of each value are just concatenated. For each element \(x_i\) we are going to store the lower \(l\) bits.
Since by definition, each element takes \(l\) bits, for a value \(x_i \qquad \forall 0 \le i < n\) the total memory needed to store the lower bits is: \[L = n l + \mathcal{O}(1) \text{bits}\]
We store these bits as contiguous array, we can efficently read and write the low bits.
High bits \(H\)
The inverted unary encoding \(\mathcal{U}: \mathbb{N} \to 0^*1\) for a given integer \(x\) is as a sequence of \(x\) 0s and then a delimiter 1, it follows that \(|\mathcal{U}(x)| = x + 1\):
| \(x\) | \(\mathcal{U}(x) = 0^x1 \) |
|---|---|
| 0 | 1 |
| 1 | 01 |
| 2 | 001 |
| 3 | 0001 |
| 4 | 00001 |
The higher-bits of each value \(x_i \quad \forall 0 \le i < n\) are \(h_i = \left\lfloor \frac{x_i}{2^l} \right \rfloor \), where \(h_0 = 0\), we can compute the number of bits used by the high-bits \(H\) as: \[\begin{aligned} H &= \sum_{0 \le i < n} |\mathcal{U}(h_{i + 1} - h_{i})| + \mathcal{O}(1)\\ &= \sum_{0 \le i < n} h_{i + 1} - h_{i} + 1 + \mathcal{O}(1)\\ &= \sum_{0 \le i < n} h_{i + 1} - h_{i} + \sum_{0 \le i < n } 1 + \mathcal{O}(1)\\ &= n + \sum_{0 \le i < n} h_{i + 1} - h_{i}+ \mathcal{O}(1)\\ \end{aligned}\]
Since it's a telescopic series, we know that:
\[\sum_{0 \le i < n} h_{i + 1} - h_{i} = h_n - h_0 = h_n - 0 = h_n\]
By recalling that \(0 \le x_n \le u\) we can finally obtainin an upperbound:
\[H = n + \left\lfloor \frac{x_n}{2^l} \right \rfloor + \mathcal{O}(1) \le n + \left\lfloor \frac{u}{2^l} \right \rfloor + \mathcal{O}(1)\]
Without loss of generality we are going to be assume that \(x_n = u\) as it's the worst case.
Optimal Threshold \(l\)
To be precise, each integer can be represented as a binary sequence using \(\lceil \log_2 u \rceil\) bits. This representations split this binary sequence into the first \(\lceil \log_2 n \rceil\) bits,called the the higher bits, and the lower \(l = \lceil \log_2 u \rceil - \lceil \log_2 n \rceil \le \left \lceil \log_2 \frac{u}{n} \right \rceil\) bits.
The total memory used by elias fano is: \[\mathcal{EF}(u, n) = H + L = n + \left\lfloor \frac{u}{2^l} \right \rfloor + nl + \mathcal{O}(1)\]
To find the optimal \(l\) we can just find the critical points of this function in \(l\): \[\frac{\partial}{\partial l} \mathcal{EF}(u, n) = 0 = n + \frac{\partial}{\partial l} \left\lfloor \frac{u}{2^l} \right \rfloor \]
For tractability proprouses we are going to approximate this by removing the floor function:
\[\frac{\partial}{\partial l} \mathcal{EF}(u, n) = n - \frac{u}{2^l} \ln(2) = 0\]
Now we can solve for \(l\):
\[\begin{aligned} n - \frac{u}{2^l} \ln(2) &= 0\\ \frac{u}{2^l} \ln(2) &= n\\ \frac{1}{2^l} &= \frac{n}{u\ln(2)}\\ 2^l &= \frac{u\ln(2)}{n}\\ l &= \log_2 \left( \frac{u\ln(2)}{n} \right)\\ l &= \log_2 \left( \frac{u}{n} \right) + \log_2 \left( \ln(2) \right) \approx \log_2 \left( \frac{u}{n} \right) - 0.528766 \\ \end{aligned}\]
As a practical approximation we are always going to use:
\[l = \left \lceil \log_2 \frac{u}{n} \right \rceil\]
Elias-Fano memory usage \(\mathcal{EF}(u, n)\)
We can recognize that this is a telescopic series, so we can simplify it by using the definition of high-bits: \[H = n + \left\lfloor \frac{u}{2^l} \right \rfloor = n + \left\lfloor \frac{u}{2^{\left \lceil \log_2 \frac{u}{n} \right \rceil}}\right \rfloor \le n + \frac{u}{2^{\log_2 \frac{u}{n}}} = n + \frac{u}{\frac{u}{n}} = 2n\]
Note that \(H\) has exactly \(n\) 1s , this implies that there will be at most \(n\) 0s. It follows that the optimal data structure to store the array \(H\) it's a simple Bitmap.
So the space used by Elias-Fano \(\mathcal{EF}(u, n)\) is composed by its higher \(H\) and lower \(L\) bits so: \[\mathcal{EF}(u, n) = H + L \le 2n + n \left \lceil \log_2 \frac{u}{n} \right \rceil\]
This means that Elias-Fano is asymptotically optimal as: \[\mathcal{EF}(u, n) \le 2n + n \left \lceil \log_2 \frac{u}{n} \right \rceil = n \log_2 \frac{u}{n} + \mathcal{O}(n) \sim_{u, n \to \infty} Z\] Therefore, we can prove that this structure uses at most 2-extra bits for element than the theoretical minimum: \[\mathcal{EF}(u, n) - Z \sim_{u, n \to \infty} 2n - \mathcal{O}(n) \le 2n\] Fano proved a better bound, this encoding uses at most half-bit for element more than the theoretical minimum, so this structure it's not a succint data-structure, but it's really close thus Vigna's name of quasi-succint data-structure.
Concurrent reads and writes
We can observe that, while the High-bits are defined on the gaps between successive values, this dependancy can be removed.
This proof will be analogous to the one about the space used by the high-bits. The position \(p_j = select(X, j)\) of the \(j\)-th 1 in the high-bits is just the sum of the lengths of all the previous codes: \[p_j = \sum_{0 \le i < j} |\mathcal{U}(h_{i + 1} - h_{i})| = h_j + j\]
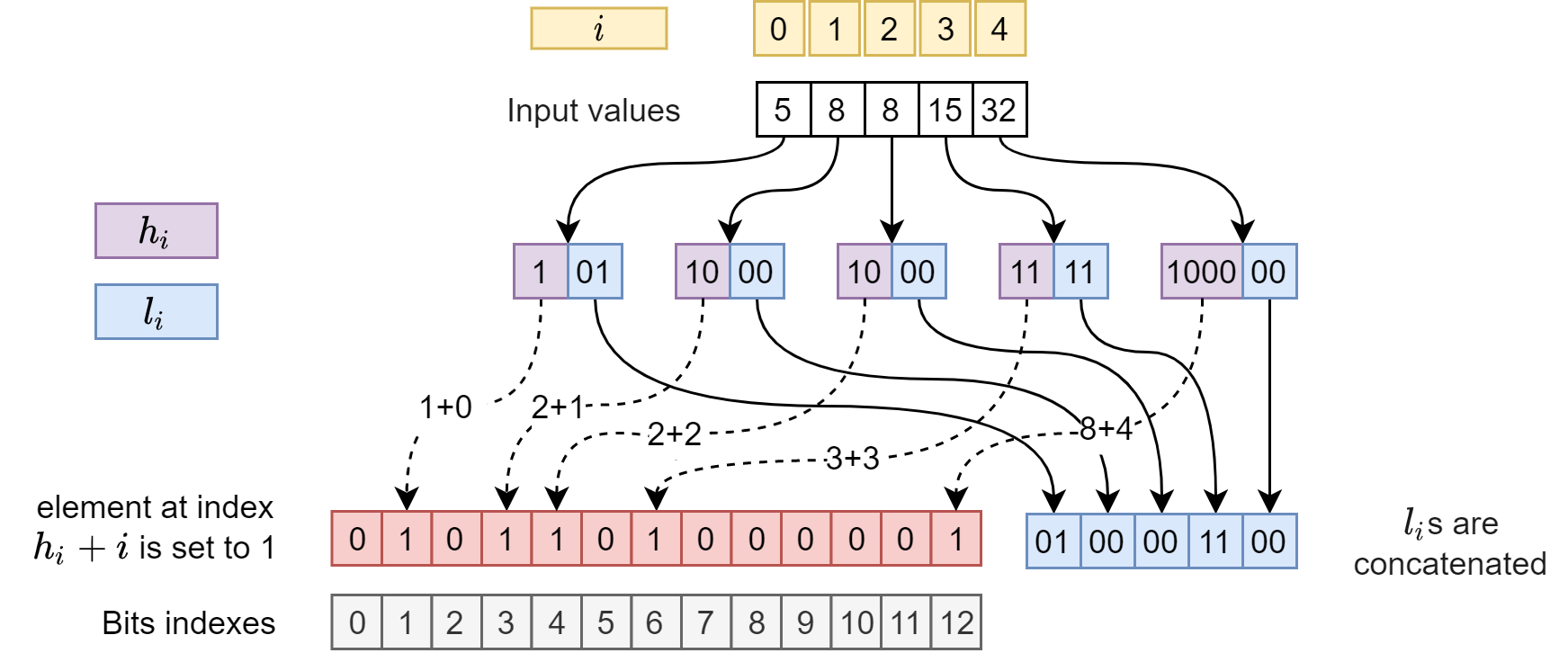
Therefore we can read and write the elias-fano structure in parallel! For a given tuple \((i, x_i)\) we now that we are going to set the high-bit \(h_i + i\) and write the low-bits in the range \([il, (i+1)l)\).
A proper implemetation requires a precise use of atomic instructions, but it's possible to create the index in parallel which can greatley speedup the loading.